다양한 활성화 함수들의 장단점
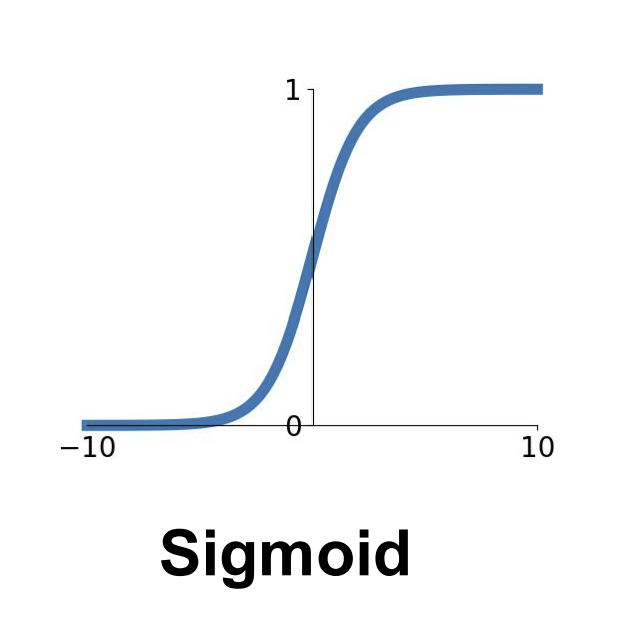
Sigmoid
(그림 1) sigmoid function
단점 1: 레이어를 깊이 쌓을 시, gradient vanishing 문제가 발생할 수 있다.
그래프를 보면 알 수 있다시피, 퍼셉트론의 출력값이 극단적으로 커지거나 작아진다면 sigmoid 함수가 포화되어 gradient가 0에 매우 가까워진다. 이에 따라 앞쪽 레이어의 gradient가 너무 작아져 학습이 안 되는 현상이 나타날 수 있다.
단점 2: Zero-centered 되어있지 않다.
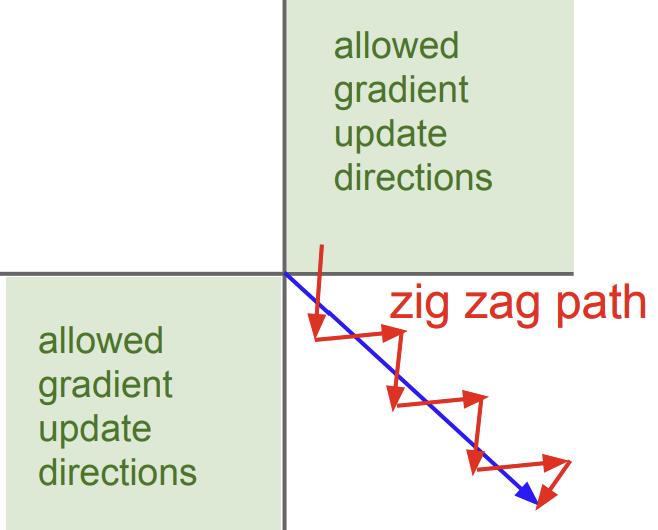
Sigmoid 함수의 출력값은 항상 양수(0에서 1 사이)이다. 따라서 (첫 레이어를 제외한) 레이어의 입력값이 모두 양수가 되는데 이게 가중치를 업데이트할 때 문제가 된다. 가중치의 gradient에는 항상 입력 값이 곱해지는데, 이에 따라 하나의 퍼셉트론 내의 모든 가중치 gradient가 같은 부호를 지니고 있기 때문이다. 즉, 퍼셉트론의 gradient들에 일종의 제한 조건이 달려 있다고 생각하면 된다.
아래 그림을 보면 퍼셉트론 내 가중치 부호가 모두 동일하다는 한계 때문에 지그재그하게 업데이트하고 있음을 알 수 있다.
(그림 2) zigzag하게 움직이는 weight
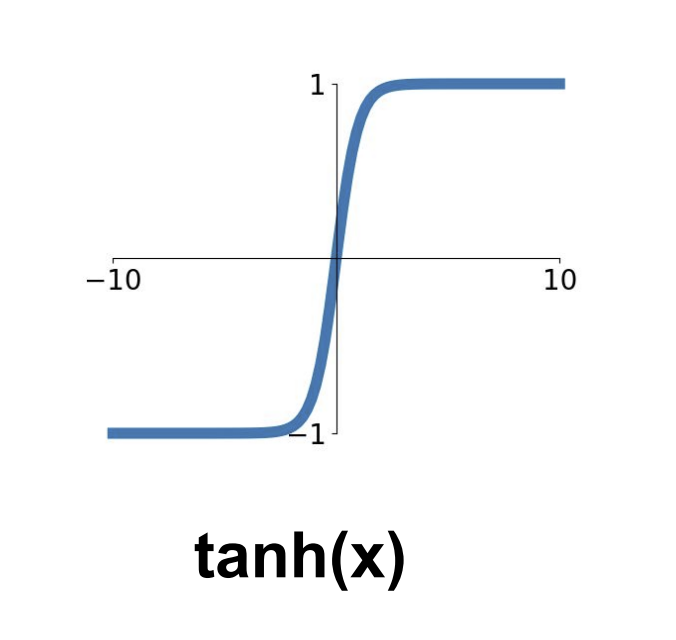
Tanh
(그림 3) tanh function
장점 1: Zero-centered 되어있다.
Sigmoid 함수와는 달리, 출력 범위가 -1에서 1까지로, 0을 중심으로 하고 있다.
단점 1: 여전히 gradient vanishing 문제가 남아있다.
여전히 입력이 크거나 작으면 출력값이 포화되어 gradient가 0에 매우 가까워지는 문제가 있다.
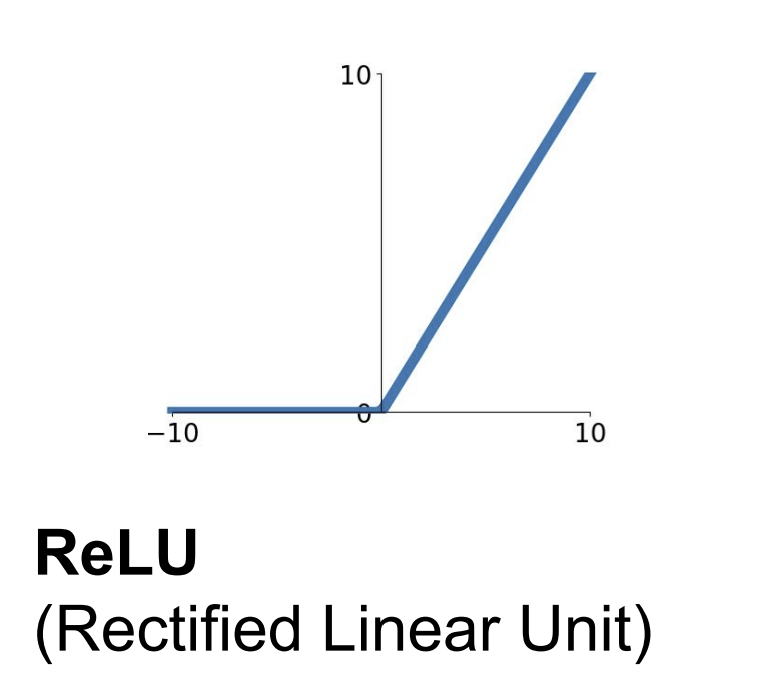
Relu
(그림 4) ReLU function
장점 1: 계산 속도가 빠르다.
연산비용이 큰 exp 함수를 사용하지 않고 간단하게 구성되었다.
장점 2: Gradient vanishing 문제를 어느 정도 해결한다.
양수 범위에서는 gradient가 1로 고정되어 전달되는 gradient가 감쇠되지 않는다.
단점 1: Zero-centered 되어있지 않다.
ReLU 함수는 오직 양수 값을 출력한다. 이는 sigmoid 함수 때와 마찬가지로 gradient가 비효율적으로 업데이트되게끔 한다.
단점 2: Dead ReLU 문제가 존재한다.
ReLU 함수의 입력이 음수라면 gradient가 0이 된다. 만약 모든 데이터에 대해서 어느 퍼셉트론이 음수를 출력하도록 하는 가중치가 세팅되었다면, 이 퍼셉트론의 gradient는 영원히 0이 되어 업데이트되지 않는다. 즉, 퍼셉트론이 죽은 것이다. 이러한 상황은 초기 가중치가 이상하게 세팅되어 있거나, learning rate가 너무 커 가중치가 극단적으로 변경될 경우 발생할 수 있다.
이를 방지하기 위해 초기 bias를 작은 양수로 세팅해두던가, ELU, Leaky ReLU 등 변형된 ReLU 함수들을 사용해 볼 수 있다.
참고자료
https://cs231n.stanford.edu/slides/2017/cs231n_2017_lecture6.pdf