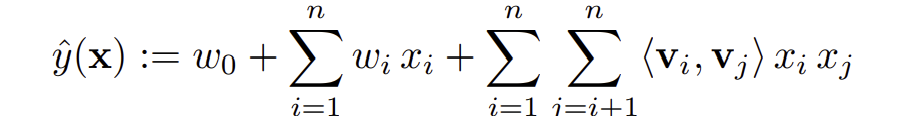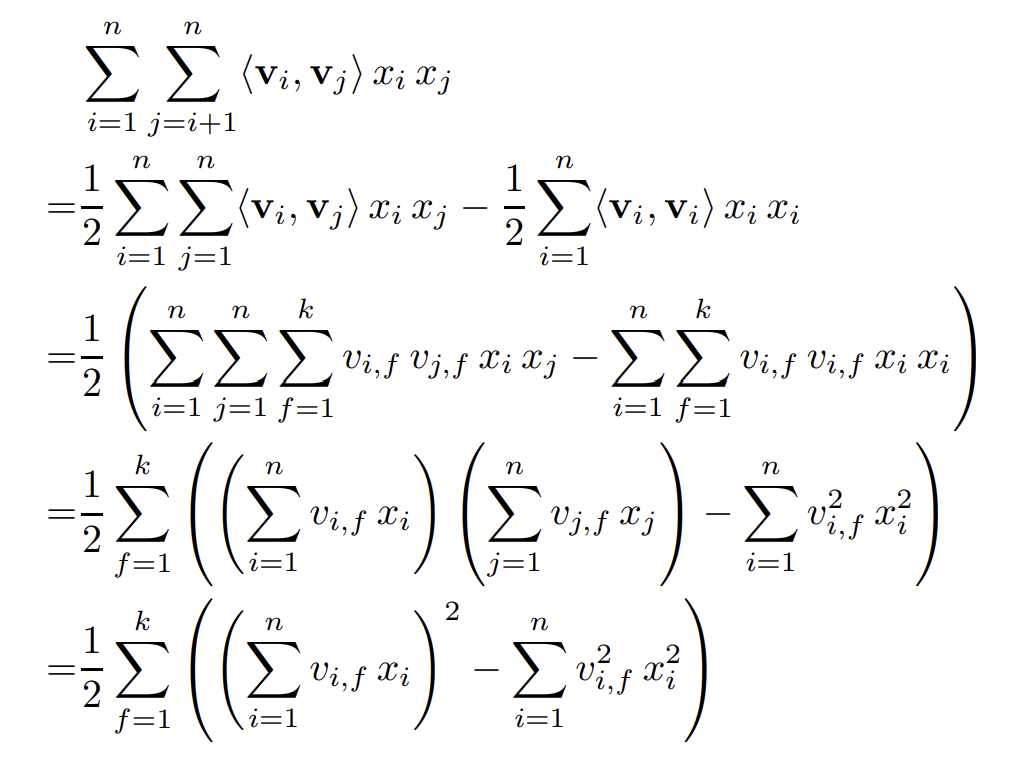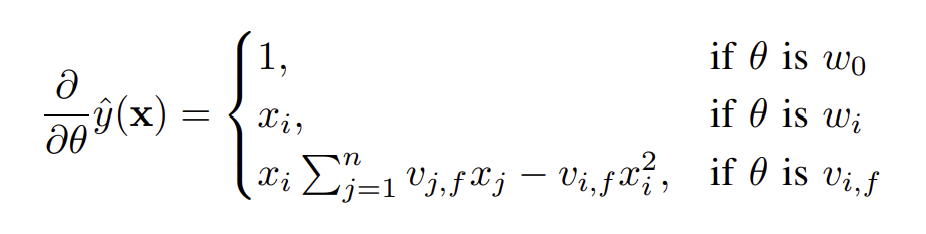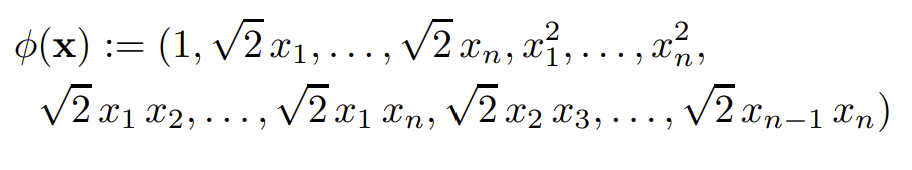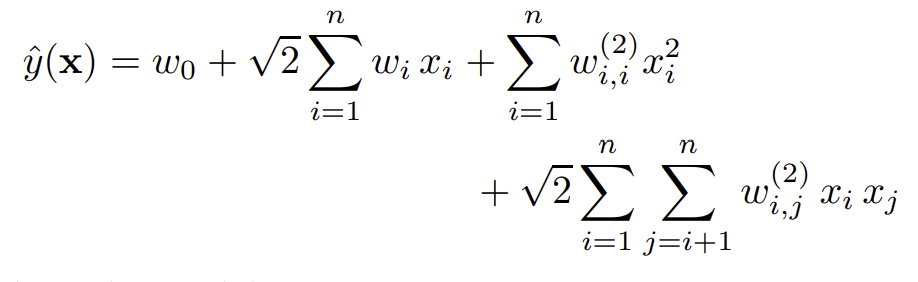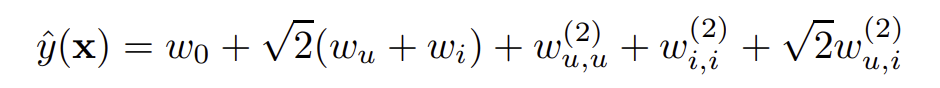Factorization Machines
‘Factorization Machines’ 논문을 간단하게 요약 정리한 글입니다.
Abstract
이 논문에서 저자는 SVM에 factorization method을 더한 Factorization Machine이라는 새로운 모델을 제시한다. FM은 SVM과 마찬가지로 특정 문제에 국한되지 않은 일반적인 predictor이지만 SVM과 달리 매우 sparse한 데이터에서도 잘 동작한다. 나아가 선형시간에 학습 및 추론이 가능하다. SVD++, PITF, FPMC와 같은 특수한 모델 또한 FM의 입력 feature만 바꿈으로써 충분히 모델링 가능하다.
Factorization Machines (FM)
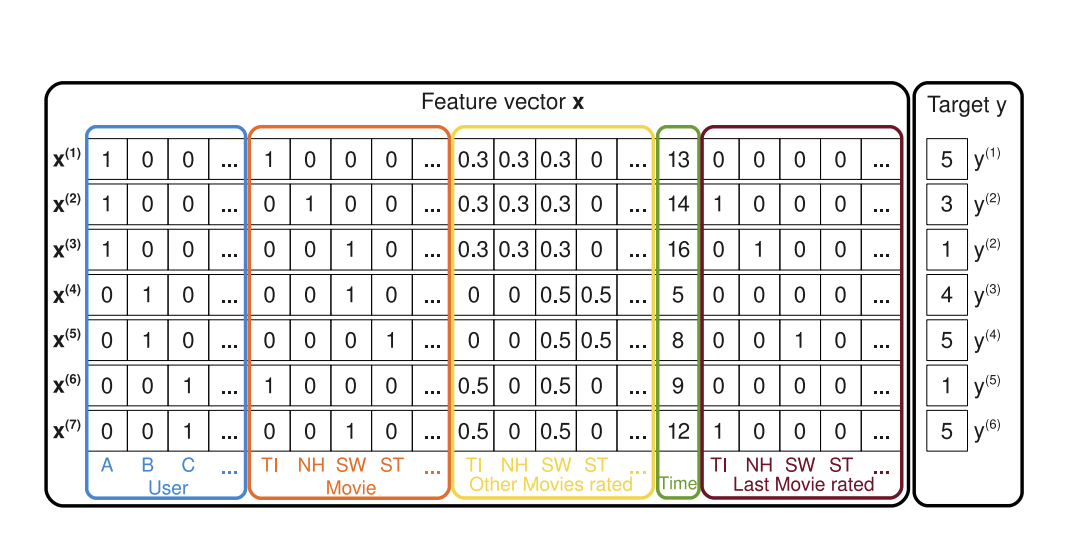
아래 그림은 FM이 각 feature vector x에 대해 학습하는 과정을 나타낸 것이다. 보다시피 FM은 일반적인 predictor로 user, movie, 시간 등 다양한 feature로부터 유저가 내릴 평가를 예측한다. 눈여겨보아야 할 점은 user와 movie가 one-hot encoding되어있기 때문에 feature 벡터가 매우 spare하다는 것이다.
degree가 2일 때의 FM의 모델은 아래 식으로 나타낼 수 있다.
식의 앞 쪽은 단순한 선형 회귀지만 중요한 점은 마지막 항이다. 마지막 항의 $v_i$와 $v_j$는 각각 feature $i$와 $j$에 대응하는 factor vector이다. FM은 이 factor vector 간의 내적을 통해 feature간의 상호작용을 모델링한다. 예를 들어, 내적이 0이라면 해당하는 feature들의 상호작용이 없다는 뜻이다.
추론 시의 시간복잡도를 생각해보자. feature간의 interaction을 계산하는 마지막 항으로 인해 시간복잡도가 $O(kn^2)$일 것 같지만 아래와 같은 방법으로 $O(kn)$안에 계산가능하다.
학습 시에도 선형시간 내에 계산이 가능하다. $\sum_{j=1}^n v_{j,f}x_j$는 i가 없기 때문에 미리 계산해놓을 수 있기 때문이다.
FM vs SVM
SVM의 커널은 데이터를 고차원의 공간으로 매핑시키는 것과 같은 역할을 해 비선형 분류도 가능하게끔 한다. kernel의 종류도 여러가지가 있는데 d = 2인 polynomial kernel은 데이터를 아래와 같이 매핑시킨다.
따라서 polynomial SVM은 다음 식으로 나타낼 수 있다.
위 식과 FM의 식은 마지막 항에서 알 수 있듯이, 두 feature간의 interaction을 모델링하고 있다는 점이 같다. 다른 부분은 parameter에 존재한다. SVM은 모든 경우의 수마다 독립적인 parameter를 두는 반면, FM은 각 feature마다 factor vector를 두어 이의 내적을 사용한다. 즉, interaction 간에 공유하는 factor가 생기게 되므로(feature i와 j 간의 interaction과 feature i와 k간의 interaction은 $v_i$를 공유한다) 이들 사이에 의존성이 생기게 된다.
FM의 이 의존성은 FM이 매우 sparse한 데이터에서도 잘 동작하게끔 한다. 먼저 SVM이 sparse한 데이터에 왜 실패하는지 알아보자. degree가 2인 polynomial kernel를 사용하고, 입력 feature로 user와 item의 one-hot vector를 사용한다고 하면 SVM의 식은 아래와 같다.
문제는 interaction을 모델링하는 parameter인 $\sqrt{2}w_{u,i}^{(2)}$에 있다. 추천 시스템의 대부분의 경우, 데이터가 spare하기 때문에 두 feature간의 interaction이 일어나는 경우가 드물다. 따라서 해당 parameter의 학습이 제대로 이뤄질 수가 없는 것이다.
반면 FM은 각 interaction을 모델링하는 parameter끼리 의존성이 존재하므로 해당 interaction이 일어나지 않아 직접적으로 학습하지 못했더라도 다른 interaction들로부터 학습된 latent factor로 충분히 모델링할 수 있다.