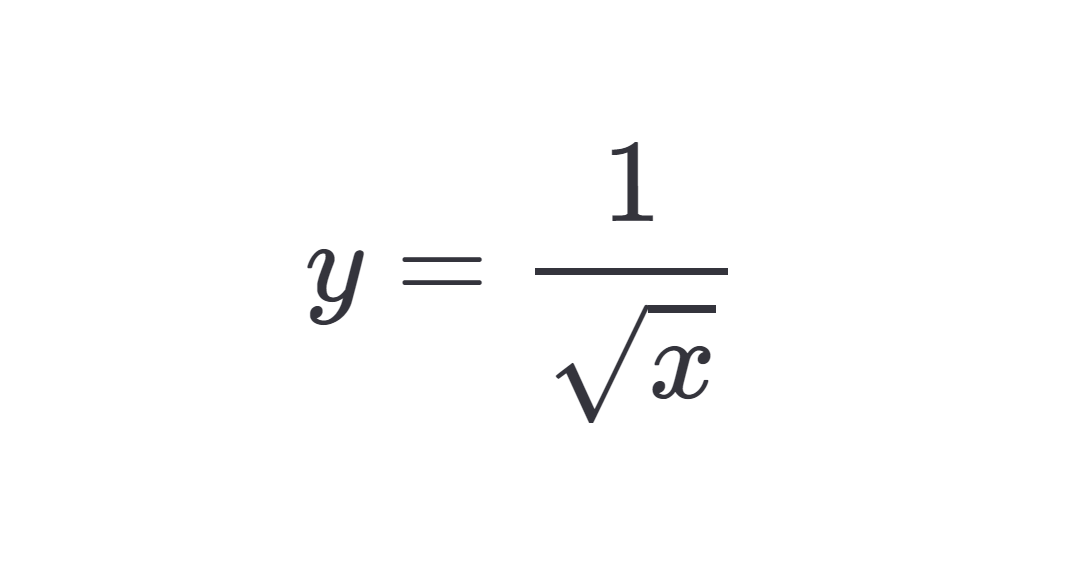Fast inverse square root

시작하기 앞서…

어떤 벡터 $v$를 유닛 벡터 $\hat{v}$으로 만들려 한다.
그러기 위해서는 다음과 같이 벡터의 크기의 역수를 $v$에 곱해 주어야 한다.

\[\hat{v} = \frac{v} {\sqrt{v_1^2 + v_2^2 + v_3^2}}\]

따라서 어떤 수의 루트의 역수를 구하는 과정이 필요하다.

\[y = \frac{1} {\sqrt{x}}\]

지금은 하드웨어 단에서 관련된 연산(SSE instruction rsqrtss)을 지원해주기 때문에 쉽고 빠르게 계산할 수 있지만 지원되기 전인 1990년도 당시에는 꽤나 부담되는 일이었다. floating point type 값들의 나눗셈이 꽤 오래 걸렸기 때문이다. 이번에 소개할 Fast inverse square root는 이러한 난관을 극복하기 위해 등장한 알고리즘으로, 현명한 비트 단위 조작을 통해 기존의 계산 방식보다 대략 4배 빠른 성능을 보여준다.

아래 코드는 게임 Quake III Arena에서 이 알고리즘을 구현한 것으로, 사실상 알고리즘이 유명해진 계기이다. 읽어보면 왜 유명해졌는지 알 수 있다…

float q_rsqrt(float number)
{
  long i;
  float x2, y;
  const float threehalfs = 1.5F;

  x2 = number * 0.5F;
  y  = number;
  i  = * ( long * ) &y;                       // evil floating point bit level hacking
  i  = 0x5f3759df - ( i >> 1 );               // what the fuck?
  y  = * ( float * ) &i;
  y  = y * ( threehalfs - ( x2 * y * y ) );   // 1st iteration
  // y  = y * ( threehalfs - ( x2 * y * y ) );   // 2nd iteration, this can be removed

  return y;
}

0x5f3759df라는 상수는 도대체 어디서 튀어나왔으며, 해괴망측한 포인터들은 무슨 의미일까?

문제 접근

---

위의 코드들을 전부 잊고 우선 input $x$와 우리가 구하고자 하는 output $y$에 관한 식을 보자.

\[y = \frac{1} {\sqrt{x}}\]

양변에 log를 씌우면 아래와 같아진다.

\[\log{(y)} = -\frac{1}{2}\log{(x)}\]

해결 방법의 윤곽이 살짝 보인다. 로그 함수와 이의 역함수만 구현하면 문제를 해결할 수 있을 것이다. ¹

\[y = \operatorname{log}^{-1}(-\frac{1}{2}\log{(x)})\]

문제는 속도다. Lookup table을 사용할 수도 있겠지만 이보다 더 메모리, 시간 측면에서 더 효율적인 방법이 있다.
바로 부동 소수점 표현을 정수형 표현으로 바라보는 방법이다. ²

float by int?

---

input $x$를 부동소수점 표현으로 바라보았을 때의 값을 $x_{float}$, 정수형 표현으로 바라보았을 때의 값을 $x_{int}$라 하자. 우선 각각의 값을 구한 후 둘 간의 관계식을 세워 이 변환이 도대체 무슨 의미를 지니는지 알아보자.

아래는 IEEE 754의 단정밀도 부동 소수점 형식이다. input $x$는 이 format에 따른다.

(source: Charles Esson, CC BY-SA 3.0, via Wikimedia Commons)

여기서 input $x$의 지수부를 \(e_x = (b_{30}b_{29} \dots b_{23})_2\)로, 가수부를 \(m_x = (0.b_{22}b_{21} \dots b_{0})_2\)로 두자.

1. $x_{float}$

IEEE 754에 따르면 $x_{float}$의 값은 다음과 같다.

\[x_{float} = 2^{e_x - 127}(1 + m_x)\]

양변에 밑이 2인 log를 씌우면 아래와 같아진다.

\[\log_2{(x_{float})} = e_x - 127 + \log_2{(1 + m_x)}\]

마지막 항이 거슬린다.
$0 < x < 1$ 일 때, $log_2{(1 + x)} \approx x$ 이므로 이를 이용하면 식을 아래와 같이 근사시킬 수 있다.

\[\log_2{(x_{float})} \approx (e_x + m_x) - 127 + \sigma\]

$\sigma$는 근사 오차의 최댓값을 최소화시키기 위한 상수로, 0.0430357로 둔다. ³

2. $x_{int}$

이제 x를 정수형 표현으로 바라봤을 때의 값인 $x_{int}$를 구해보자.
$x_{int} = (b_{30}b_{29} \dots b_{0})_2$ 이지만 $m_x$와 $e_x$로 아래와 같이 표현될 수도 있다.

\[\begin{aligned} x_{int} &= 2^{23}e_x + 2^{23}m_x \\ &= 2^{23}(e_x + m_x) \end{aligned}\]

3. 관계식

마지막으로 $x_{float}$와 $x_{int}$간의 관계식을 세워보자.
$e_x + m_x \approx \log_2{(x_{float})} + 127 - \sigma$ 이므로 이를 바로 위 식에 대입하면

\[\begin{aligned} x_{int} &\approx 2^{23}(\log_2{(x_{float})} + 127 - \sigma) \\ &\approx 2^{23}\log_2{(x_{float})} + 2^{23}(127 - \sigma) \end{aligned}\]

즉, 부동 소수점으로 표현된 값을 정수형으로 바라보면 밑이 2인 log를 씌운 뒤 이를 특정 값만큼 scale, shift한 값이 된다.

식을 다시 정리하면 아래와 같이 된다.

\[\log_2{(x_{float})} \approx \frac{x_{int}}{2^{23}} - (127 - \sigma)\]

이제 로그함수를 간단한 과정으로 구현할 수 있다는 것을 알았다!

최종 식

---

이제 처음으로 돌아가서 input $x$와 output $y$ 간의 항등식을 보자.

\[\log{(y)} = -\frac{1}{2}\log{(x)}\]

log의 밑은 상관없고 $x$와 $y$는 모두 실수형이므로

\[\log_2{(y_{float})} = -\frac{1}{2}\log_2{(x_{float})}\]

이제 우리가 구한 $log_2{(x)}$의 식을 사용하면

\[\frac{y_{int}}{2^{23}} - (127 - \sigma) = -\frac{1}{2}(\frac{x_{int}}{2^{23}} - (127 - \sigma))\]

이를 정리하면 아래와 같다.

\[\begin{aligned} y_{int} &= -\frac{1}{2} x_{int} + \frac{3}{2} 2^{23} (127 - \sigma) \\ &\approx -\frac{1}{2} x_{int} + 1597488309(\texttt{0x5F37BCB5}) \end{aligned}\]

이로써 $x_{int}$를 통해 $y_{int}$를 구할 수 있으며, $y_{int}$를 부동 소수점 형식으로 바라본 값인 $y_{float}$를 최종적으로 구할 수 있게 된다.

정리 및 결론

---

정리해보자면, 부동 소수점 형식에 따르는 어떤 실수의 제곱근에 대한 역수를 얻는 방법은 다음과 같다.

1. 부동 소수점 형식을 정수형으로 바라본다. ($x_{float} \rightarrow x_{int}$)
2. 0x5F37BCB5에 그 값의 절반을 뺀다. ($y_{int} = \texttt{0x5F37BCB5} - \frac{1}{2} x_{int}$)
3. 정수형을 부동 소수점 형식으로 바라본다. ($y_{int} \rightarrow y_{float}$)

코드로 돌아가 선언 다음에 등장하는 첫 세 줄을 살펴보자. 상수 0x5F37BCB5가 조금 더 근사 오차를 줄여주는 0x5F3759DF로 변한 것만을 제외하면 전체적인 과정은 동일하다는 것을 알 수 있다.

  i  = * ( long * ) &y;                       // evil floating point bit level hacking
  i  = 0x5f3759df - ( i >> 1 );               // what the fuck?
  y  = * ( float * ) &i;

사실 알고리즘의 마지막 줄은 설명하지 않았다.
이는 근사 오차를 줄여주는 일반적인 방법인 Newton’s method를 적용한 것으로, 흥미가 있다면 아래 참고 자료에 있는 위키 페이지에 들어가 더 읽어보시길…

  y  = y * ( threehalfs - ( x2 * y * y ) );   // 1st iteration
  // y  = y * ( threehalfs - ( x2 * y * y ) );   // 2nd iteration, this can be removed

참고 자료

https://en.wikipedia.org/wiki/Fast_inverse_square_root

---

1. 편의를 위해 아래 식에서 log함수의 역함수를 부정확하게 표현하였다. ↩

2. 데이터는 변경되지 않는다. 데이터를 바라보는 관점만 바꾼다는 것이다! ↩

3. 단, 이 값은 이후의 단계들을 고려하지 않고 계산한 값으로, 전체 문제에 있어서 최적의 값이 아니다. ↩