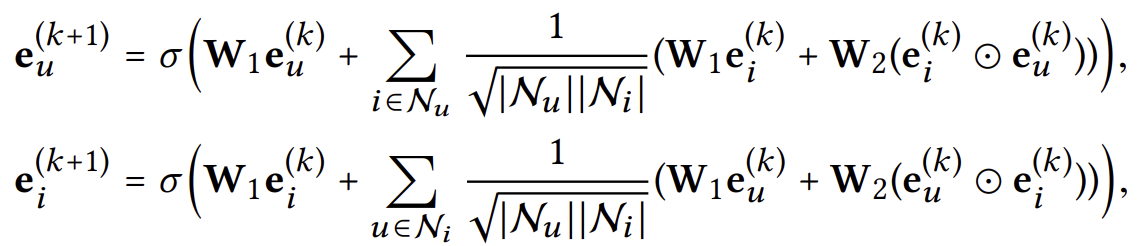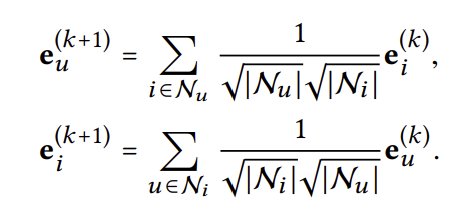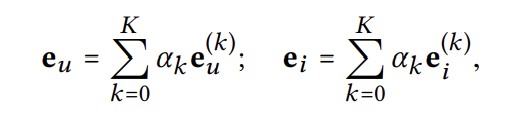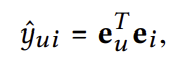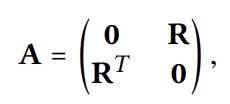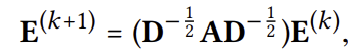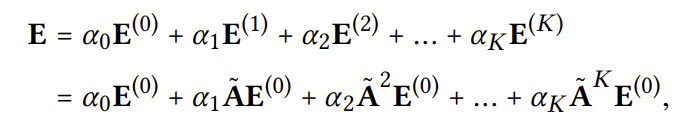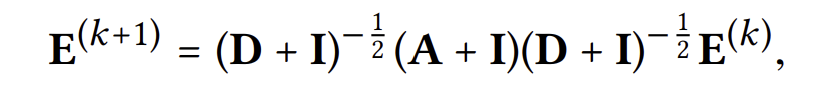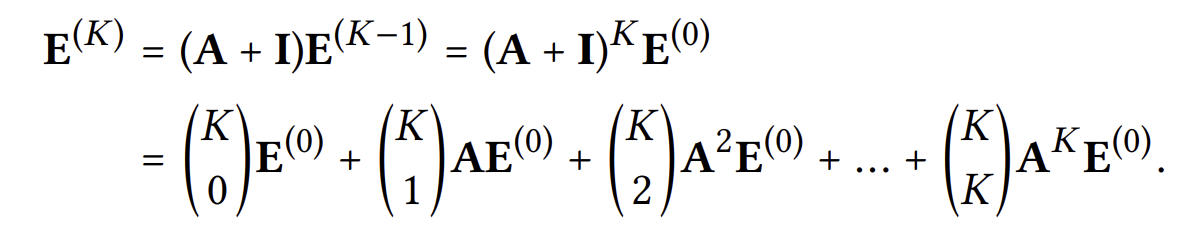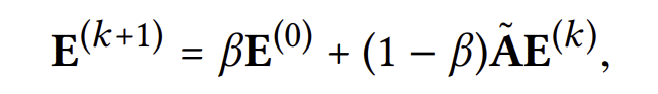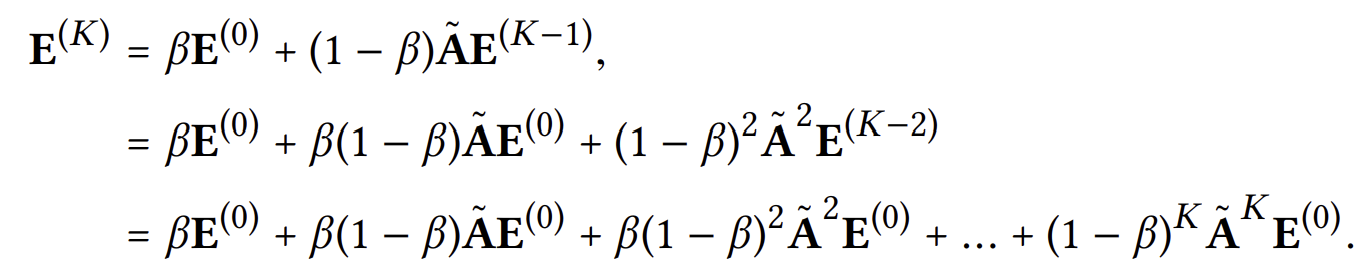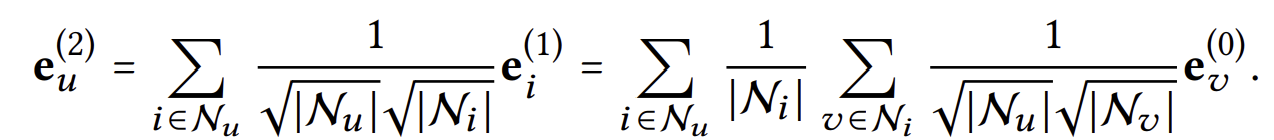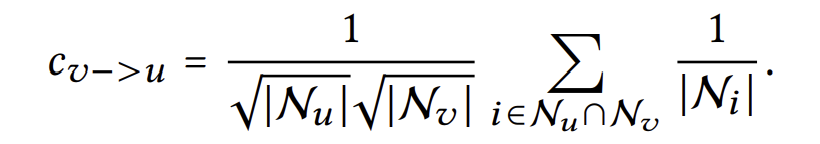LightGCN
‘LightGCN: Simplifying and Powering Graph Convolution Network for Recommendation’ 논문을 간단하게 요약 정리한 글입니다.
Abstract
Graph Convolution Network(GCN)은 collaborative filtering에 있어서 새로운 SOTA 모델이 되었다. 하지만 GCN은 본래 그래프 상에서의 분류 문제를 위한 모델로, 추천 시스템에 적용함에 있어서 불필요한 요소들에 대한 분석이 제대로 이루어지지 않았다. 저자는 GCN의 비선형 활성화 함수와 가중치 행렬을 통한 특성 변환이 불필요하다고 주장한다. 나아가 GCN의 핵심인 neighborhood aggegation만을 남긴 LightGCN을 제시한다.
Preliminaries
NGCF는 대표적인 SOTA GCN model이다. $e^{(0)}_u$와 $e^{(0)}_i$가 각각 유저 u와 아이템 i에 대한 임베딩이라 할 때, NGCF는 이를 아래와 같이 변환시킨다.
저자는 이 식의 행렬 $W_1$과 $W_2$, 그리고 비선형 활성화 함수 $\sigma$가 불필요하다고 주장한다. 많은 정보를 임베딩해야하는 노드 분류 문제 때와는 달리, 오직 유저 또는 아이템의 ID를 임베딩하는 것이기 때문에 가중치 행렬을 통한 복잡한 변환은 과하고, 오히려 학습을 방해한다는 것이다.
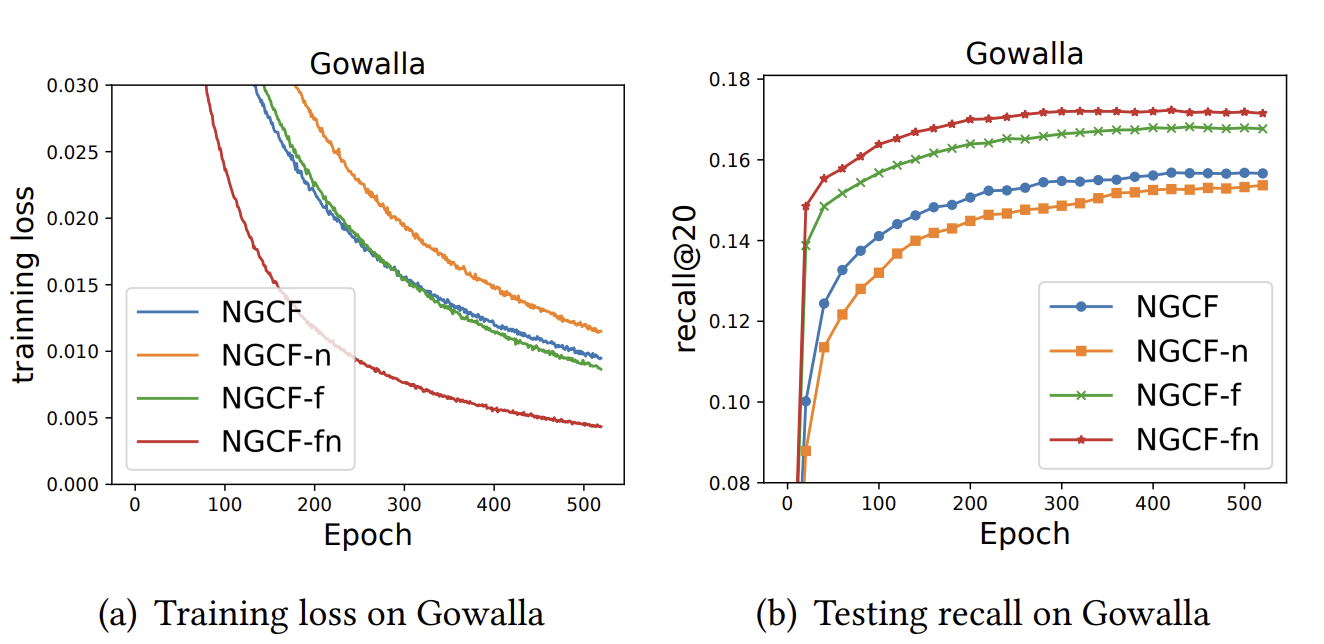
저자는 이를 보여주기 위해 NGCF의 3가지 변형을 실험해본다.
- NGCF-f, 가중치 행렬 $W_1$과 $W_2$를 제거한 버전
- NGCF-n, 비선형 활성화 함수 $\sigma$를 제거한 버전
- NGCF-fn, 둘 다 제거한 버전
NGCF는 NGCF-f보다 더 높은 표현력을 가지고 있다. 단순히 $W_1$과 $W_2$를 항등 행렬 $I$로 만들면 NGCF-f가 되기 때문이다. 하지만 NGCF-f는 NGCF보다 test와 train 모두에 있어서 더 나은 성능을 보인다. 이로부터 가중치 행렬을 통한 특성 변환이 오히려 NGCF의 학습을 방해한다는 사실을 알 수 있다.
LightGCN
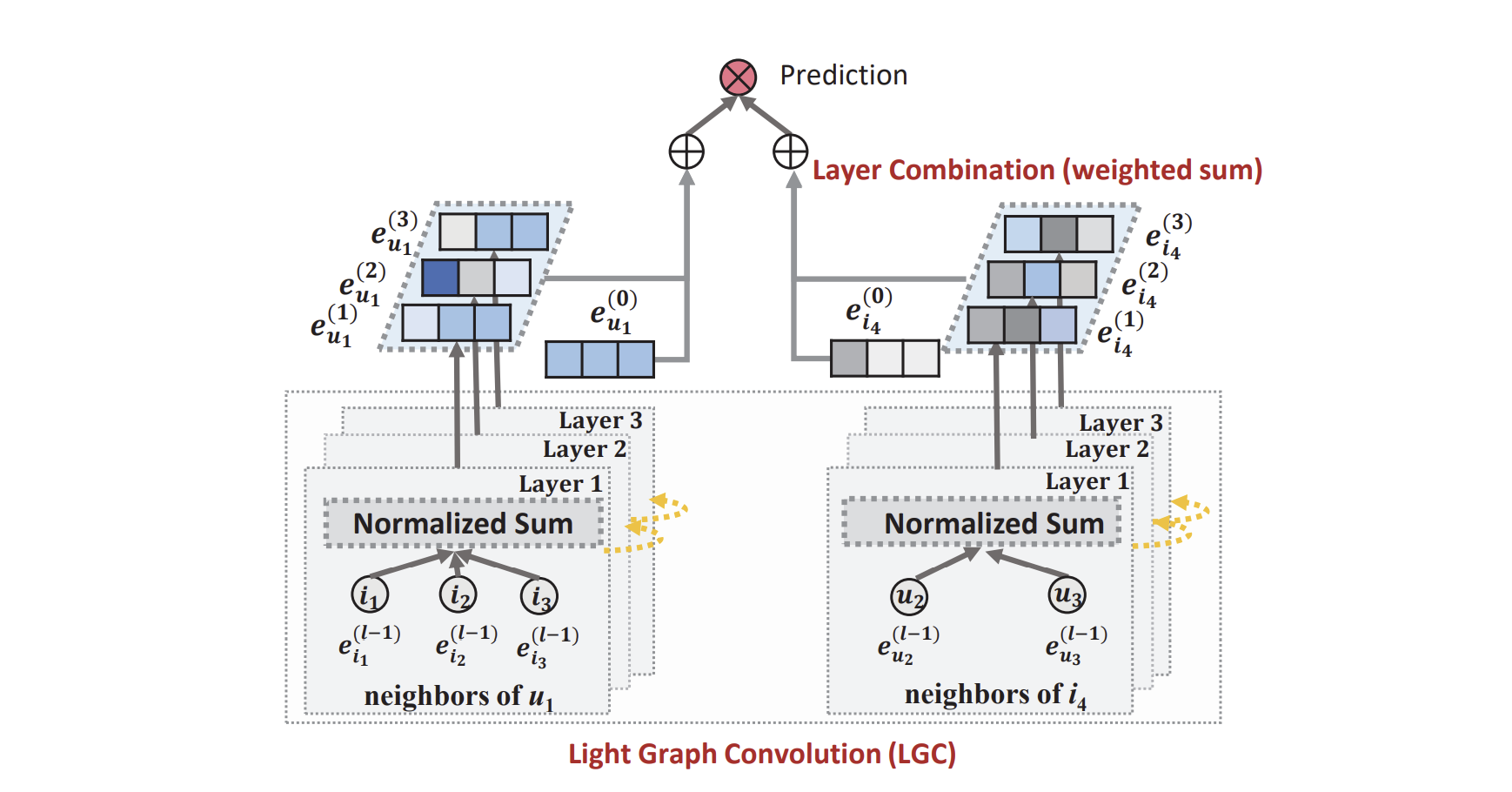
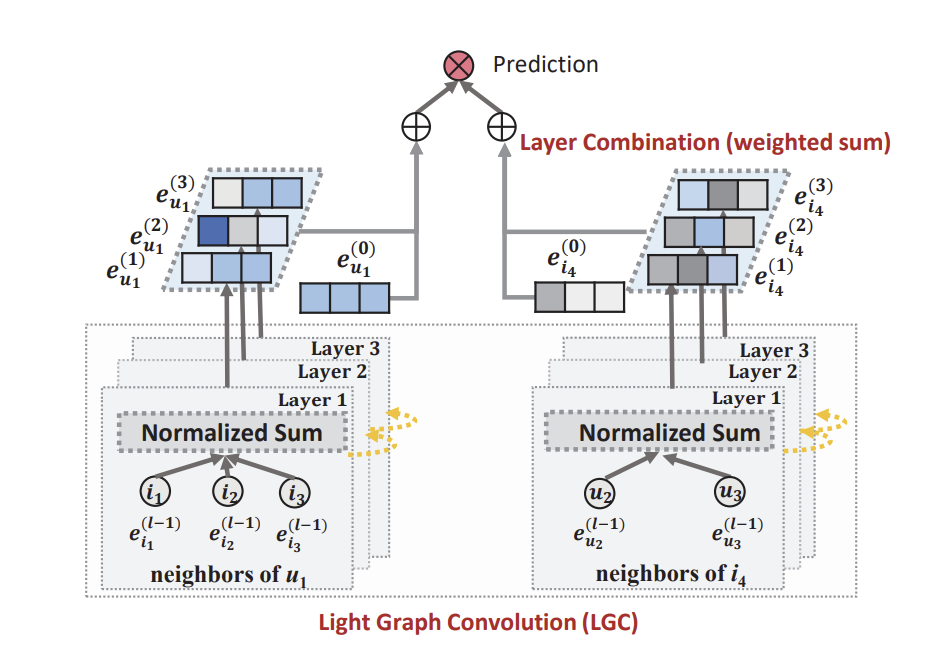
이러한 사실들에 기반하여, 저자들은 경량화한 GCN 모델인 LightGCN을 제안한다.
구체적으로, 모델은 아래 순서와 같은 과정을 거친다.
각 유저와 아이템에 대한 첫 임베딩 $e_u^{(0)}$과 $e_i^{(0)}$을 초기화한다. 이는 모델이 학습할 수 있는 유일한 파라미터이다.
레이어를 여러번 거침으로써 임베딩을 변화시킨다. 레이어를 한번 거치면 어느 임베딩 벡터는 단순히 주변 임베딩 벡터들의 가중 합이 된다. 가중 합을 계산할 때 자기 자신은 포함시키지 않는다.
각 레이어 별로 나온 임베팅 벡터의 가중 합을 최종 임베딩 벡터로 한다. 가중치 $a_k$는 기본적으로 1로 두지만 이는 변경 가능하다.
임베딩된 아이템 벡터와 유저 벡터를 내적함으로써 점수를 계산한다.
이를 행렬을 통해 간단히 나타낼 수도 있다.
먼저 user-item의 상호작용 그래프 $A$를 정의해보자.
$A$의 $i$번째 행벡터에 존재하는 0이 아닌 원소의 개수를 $i$열 $i$행의 원소로 하는 대각 행렬을 $D$라 할 때, 임베딩 벡터는 아래와 같이 계산된다.
마지막으로, 최종 임베딩 벡터는 모든 레이어들로부터 나온 임베딩 벡터의 가중 합으로 둔다.
(이때 $\widetilde{A} = D^{-\frac{1}{2}} A D^{-\frac{1}{2}}$)
Model Analysis
LightGCN 모델이 왜 이렇게 구성되었는지 알아볼 것이다.
1. self-connection의 부재
LightGCN 모델의 레이어가 임베딩 벡터를 계산할 때, 해당 벡터의 이전 임베딩 값은 고려하지 않는다. 즉, user-item의 상호작용 그래프에서 self-connection이 존재하지 않는다는 것이다. 이는 어떻게 보면 비직관적일 수 있지만, 사실 각 레이어 별로 나온 임베딩 벡터를 적절히 합쳐 최종 임베딩 벡터를 만드는 과정이 self-connection의 추가를 생략해도 무방하게끔 해준다.
아래와 같이 self-connection을 추가로 고려해 임베딩 벡터를 계산한다고 해보자.
$(D + I)^{-\frac{1}{2}}$는 단순히 scaling factor이므로 무시한다면, 마지막 레이어로부터 나온 임베팅 벡터는 아래와 같아진다.
즉, self-connection을 추가하는 것은 이전 임베딩 벡터들의 가중 합을 최종 임베딩 벡터로 두는 것과 사실상 동일하다.
2. over-smoothing?
레이어를 쌓을수록 가중 평균 연산들이 반복되고 이에 따라 임베딩 벡터들이 over-smoothing될 것이라고 걱정해볼 수 있다. 하지만 이 역시 각 레이어 별로 나온 임베딩 벡터를 합치는 과정을 통해 해결된다.
over-smoothing되지 않도록 아래 식과 같이 첫 임베딩을 일부 유지하도록 식을 수정했다고 해보자.
이제 최종 레이어로부터 나온 임베딩 벡터를 계산해보면 아래와 같아진다.
즉, 이전 레이어들의 가중 합을 임베딩 벡터로 두는 과정은 위와 같이 over-smoothing을 방지하는 역할 또한 한다는 것을 알 수 있다.
3. smoothness의 해석
각 레이어를 거침에 따라 임베딩 벡터들이 얼마다 smooth해지는지도 해석가능하다. 레이어가 2개 존재하는 LightGCN을 생각해보자. 마지막(2번째) 레이어로부터 나온 임베딩 벡터는 아래와 같이 계산가능하다.
즉, 유저 v가 유저 u에 영향을 주는 정도(smoothness의 강도)는 아래와 같이 보일 수 있다.
이 값은 직관적으로 쉽게 해석가능하다.
- 공통으로 상호작용한 아이템이 많을수록 강도는 강해진다.
- 공통으로 상호작용한 아이템의 인기가 낮을수록, 강도는 강해진다.
- 유저가 상호작용한 아이템이 적을수록, 강도는 강해진다.