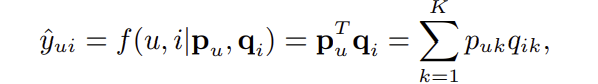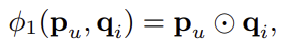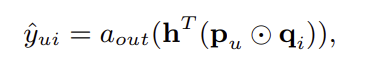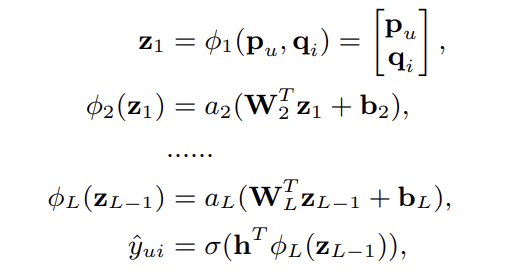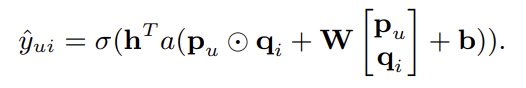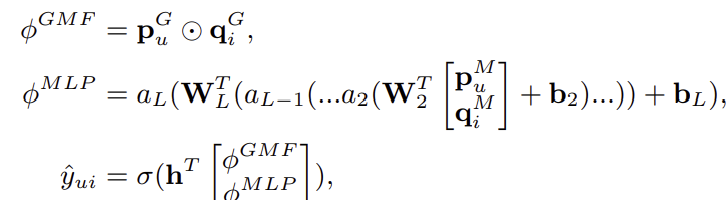Neural Collaborative Filtering
‘Neural Collaborative Filtering’ 논문을 간단하게 요약 정리한 글입니다.
Abstract
추천 시스템 분야에서 deep neural network의 사용은 상대적으로 적은 관심을 받아왔다. 지금까지 아이템 벡터와 유저 벡터 간의 상호작용은 두 벡터의 내적을 통해 계산해왔는데, 저자들은 이를 neural network로 대체한 Neural Collaborative Filtering(NCF)을 제안한다. 이러한 NCF는 일반적인 MF를 충분히 표현할 수 있으면서도 neural network를 통해 non-linear한 관계의 모델링 또한 가능하다.
Possible Limitations of MF
MF 모델은 아래 식과 같이 유저 벡터와 아이템 벡터의 내적을 통해 상호작용을 선형적으로 모델링한다.
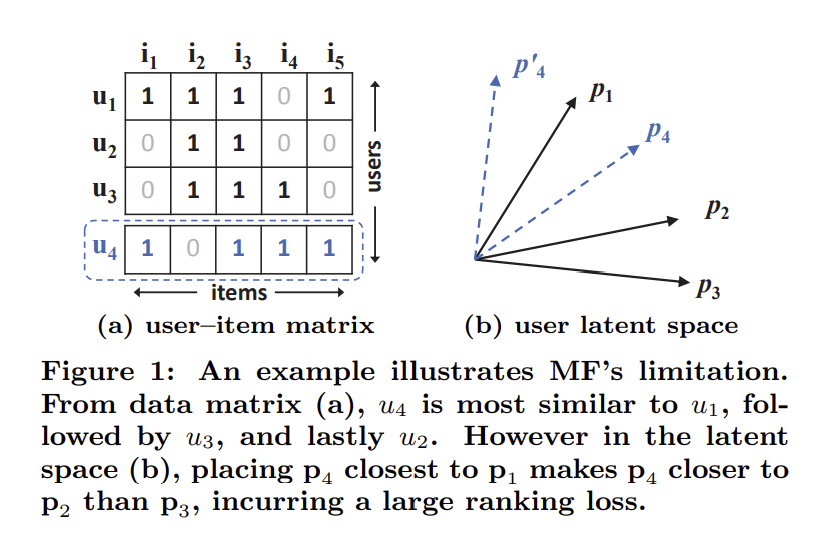
아래 그림은 MF 모델이 표현할 수 있는 한계를 직관적으로 보여준다. 먼저, 표 1-a에 존재하는 유저 1, 2, 3의 유사도를 계산해보자. $s_{ij}$가 유저 i와 j의 유사도를 나타낸다고 할 때, $s_{23}(0.66) > s_{12}(0.5) > s_{13}(0.4)$이다. 따라서 유저들의 벡터는 그림 1-b와 같이 둘 수 있을 것이다. 하지만 여기서 유저 4가 등장했다고 해보자. 각 유저들의 유저 4에 대한 유사도는 $s_{41}(0.6) > s_{43}(0.4) > s_{42}(0.2)$로, 즉 유저 4는 유저 1과 가장 가깝고 유저 2와 가장 멀다. 그러나 유저 4를 그림 1-b에 어떤식으로 놓아도 이러한 유사도를 표현할 수 없다.
물론 이러한 한계는 latent factor의 크기인 K를 늘림으로써 해결할 수 있지만, 그럴 경우 overfitting에 취약하게 된다. 따라서 저자들은 MF 모델의 표현력의 한계를 deep neural network를 통해 해결하고자 한다.
Neural Collaborative Filtering
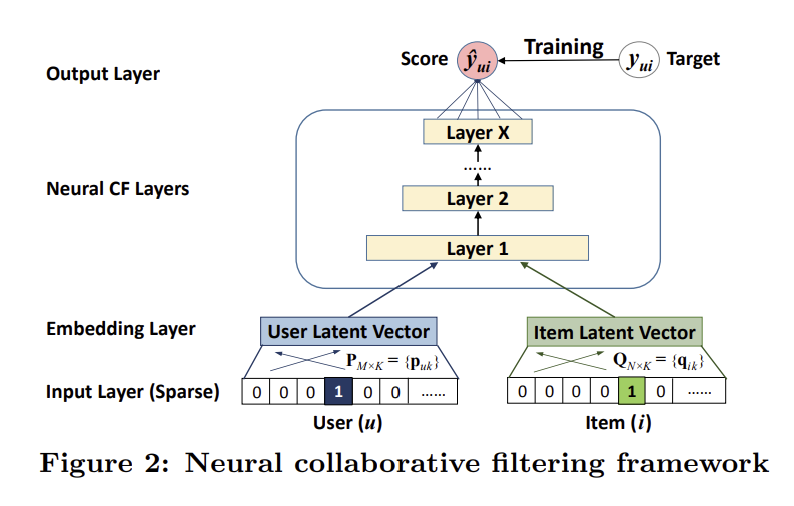
NCF의 기본적인 프레임워크는 아래의 그림 2와 같다.
아래에서부터 차례대로 설명하자면, NCF는 먼저 input layer에서 유저와 아이템을 표현하는 feature 벡터를 각각 받는다. 이 feature 벡터는 content 기반으로 구성될 수도 있지만, 논문에서는 단순 one-hot 벡터로 두어 순수한 collaborative filtering에 집중하도록 하였다. 이후, 각각의 feature 벡터는 embedding layer를 통과하여 일종의 latent factor로 표현된다. 이 embedding layer는 fully connected layer로, sparse한 feature 벡터를 dense한 latent 벡터로 변환한다. 그런 다음 이 두 벡터는 non-linear한 관계의 모델링을 위해 여러개의 neural network layer를 통과한다. 이러한 layer를 논문에서는 neural collaborative filtering layer라고 명명하였다. 최종적인 output layer에서는 마지막 layer의 output을 상호작용의 예측값 $\hat{y_{ui}}$로 변환한다. 이러한 예측값을 통해 pointwise loss나 pairwise loss를 계산할 수 있고, 이를 최소화하는 방향으로 학습을 진행한다.
Generalization of Matrix Factorization
MF는 NCF 프레임워크의 특별한 경우로 볼 수 있다. Embedding layer를 통과한 유저 벡터와 아이템 벡터를 각각 $p_u$와 $q_i$라고 하자. $p_u = P^T v^U_u$, $q_i = Q^T v^I_i$로 표현되게끔 embedding layer를 둘 수 있다. 이때 $P$와 $Q$는 각각 유저와 아이템의 embedding matrix이고, $v^U_u$와 $v^I_i$는 각각 유저와 아이템의 one-hot 벡터이다. 이렇게 되면 NCF의 embedding layer는 MF의 embedding layer와 동일하다.
나아가 첫번째 neural collaborative filtering layer는 아래와 같이 둔다.
여기서 ⊙는 element-wise product를 나타낸다.
마지막으로 output layer는 아래와 동일하게 설정한다.
여기서 $a_{out}$과 $h$는 각각 activation function과 latent factor의 각 dimension에 대한 weight을 나타낸다. 만약 activation function을 identity function으로 두고 $h$를 1로 구성된 uniform vector로 둔다면 이는 결국 MF와 동일한 형태가 된다. 눈여겨 보아야 할 점은, NCF를 통해 구현된 MF는 쉽게 확장될 수 있다는 것이다. 예를 들어 $h$를 학습시에 업데이트 가능한 parameter로 두거나 activation function을 non-linear한 함수로 둠으로써, 다양한 종류의 MF 모델을 구현할 수 있다.
Multi-Layer Perceptron
NCF 프레임워크의 또다른 구현 방법은 multi-layer perceptron(MLP)을 사용하는 것이다. 이 경우, neural collaborative filtering layer는 아래와 같이 표현된다.
여기서 $W_x$, $b_x$, $a_x$는 각각 $x$번째 layer의 weight matrix, bias vector, activation function을 나타낸다. 이러한 MLP를 통해 non-linear한 관계를 모델링할 수 있다.
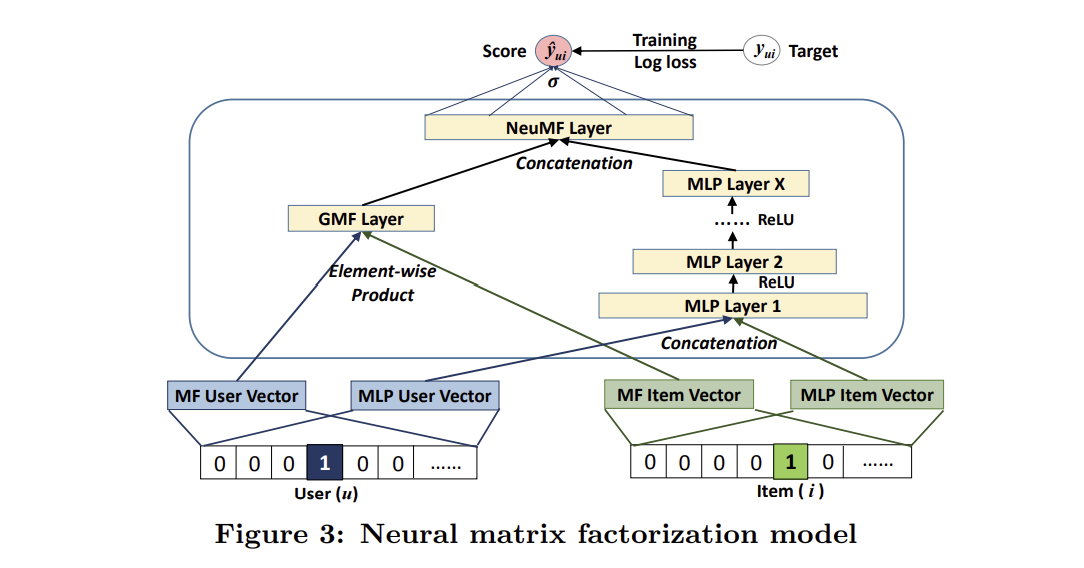
Fusion of GMF and MLP
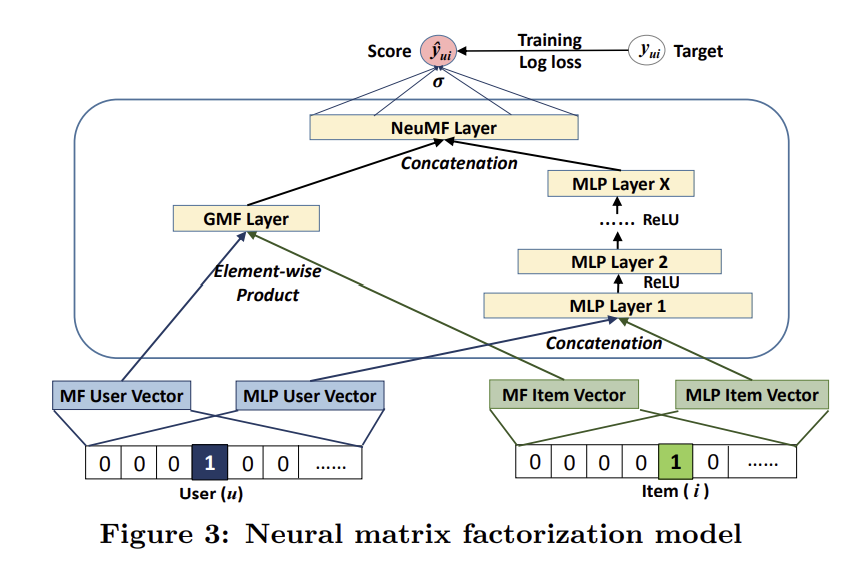
지금까지 NCF의 구현체로 GMF와 MLP를 소개했는데, 이 둘을 합침으로써 서로간의 단점을 보완해볼 수 있을 것이다. 가장 직관적인 방법은 이 두 모델이 서로 같은 embedding layer를 공유하도록 하고 output layer 직전에 합하는 것이다. 이러한 방식은 아래와 같이 표현된다.
하지만, GMF와 MLP마다 최적의 embedding size가 다르기에 이 방식이 최적의 앙상블로 볼 수는 없다. 따라서 각 모델마다 embedding size를 다르게 하고, output layer 직전에 concatenate하는 방식을 사용할 수도 있다. 이는 아래와 같이 표현된다.
여기서 $p^G_u$와 $p^M_u$는 각각 GMF와 MLP의 유저 embedding 벡터이며, $q^G_i$와 $q^M_i$는 각각 GMF와 MLP의 아이템 embedding 벡터이다. 이러한 방식을 통해 MF의 linearity과 MLP의 non-linearity를 동시에 활용할 수 있게 되며 이 앙상블 모델을 저자들은 NeuMF라 명명하였다.