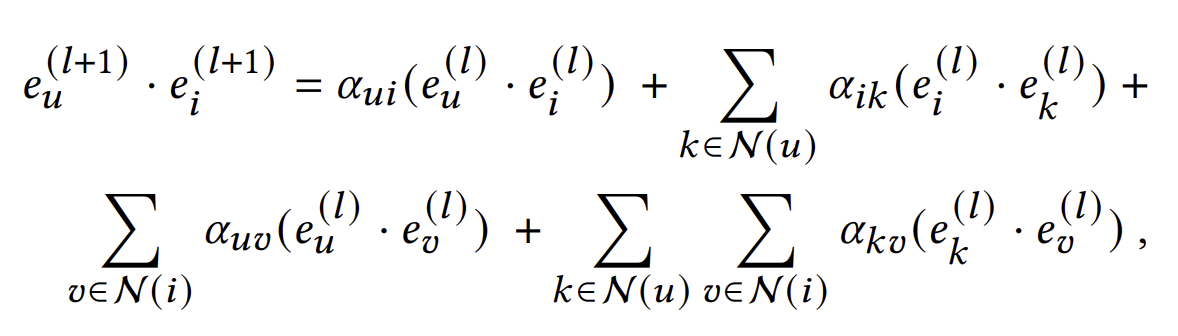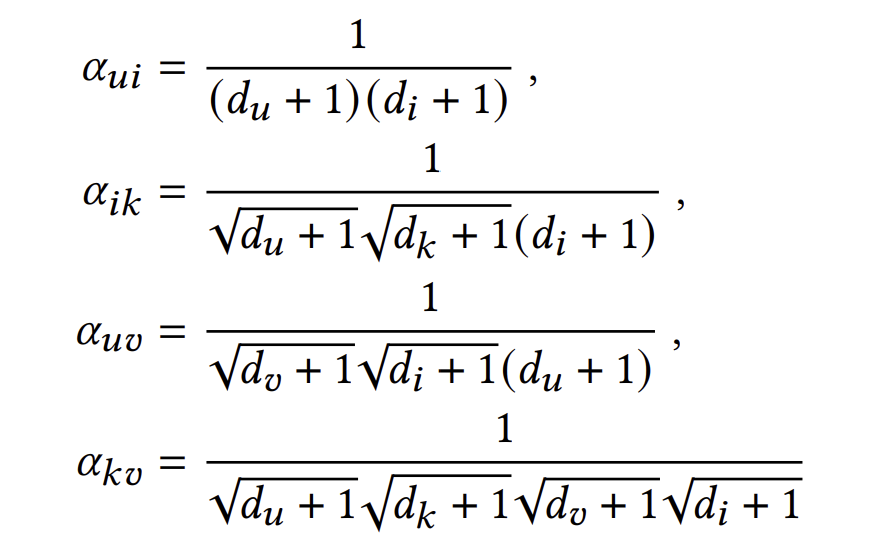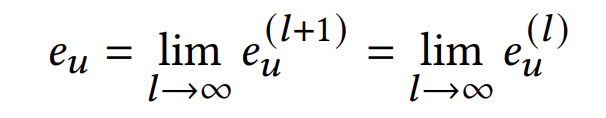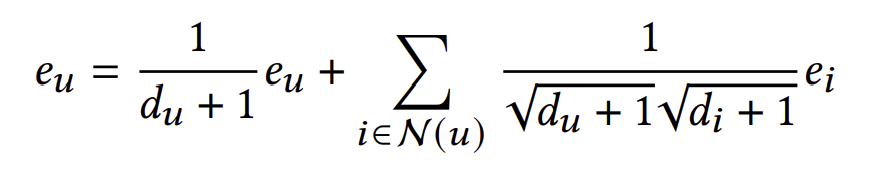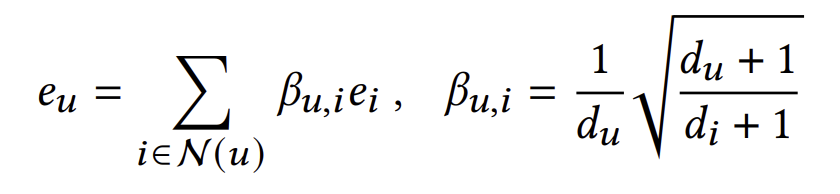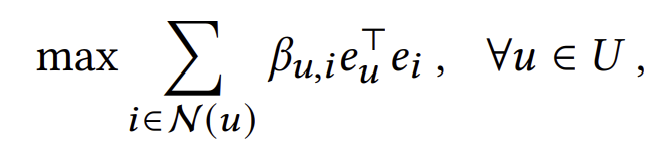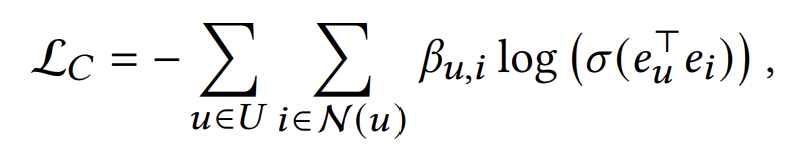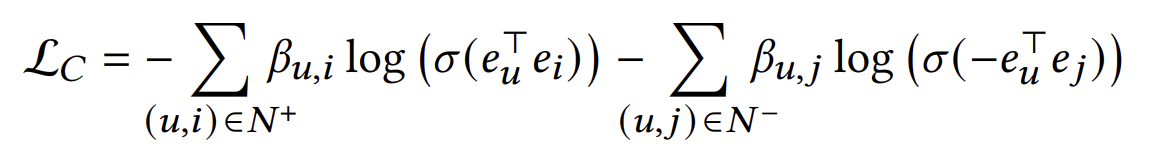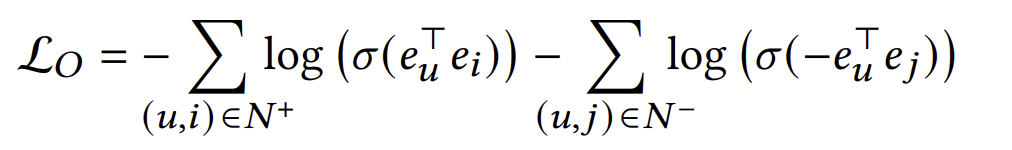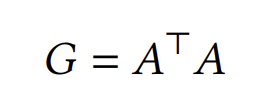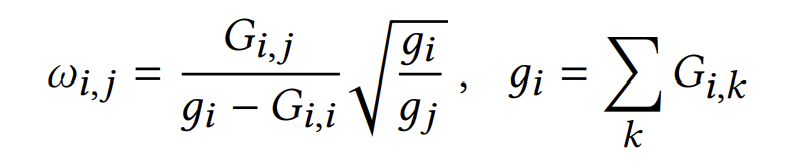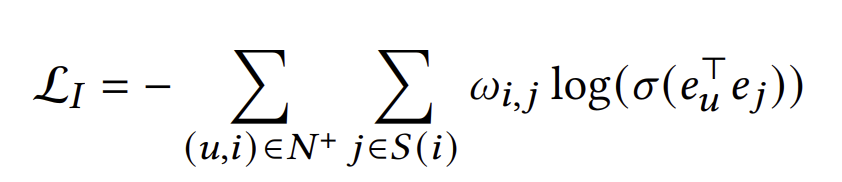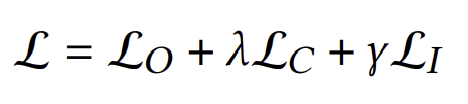UltraGCN
‘UltraGCN: Ultra Simplification of Graph Convolutional Networks for Recommendation’ 논문을 간단하게 요약 정리한 글입니다.
Abstract
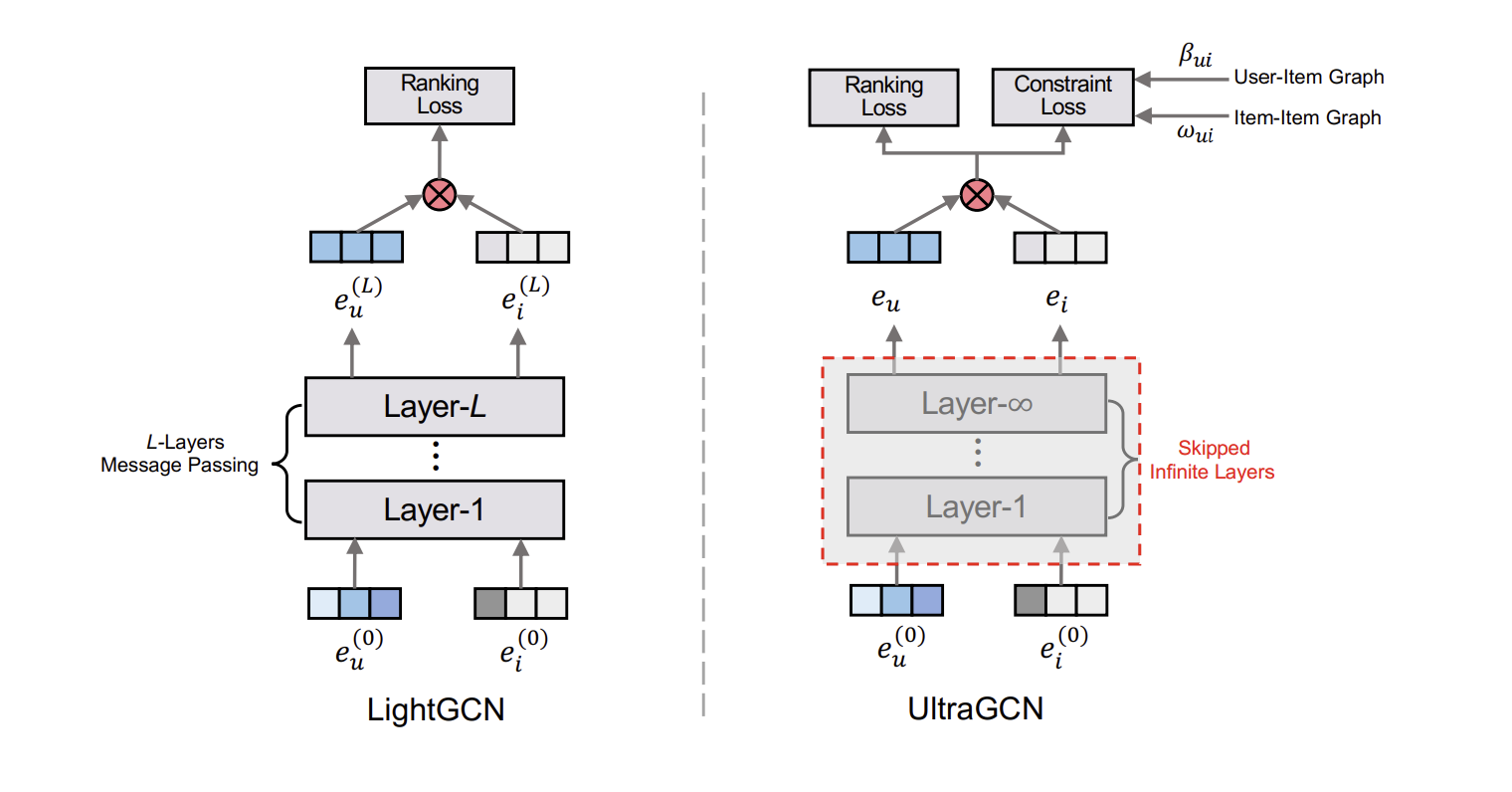
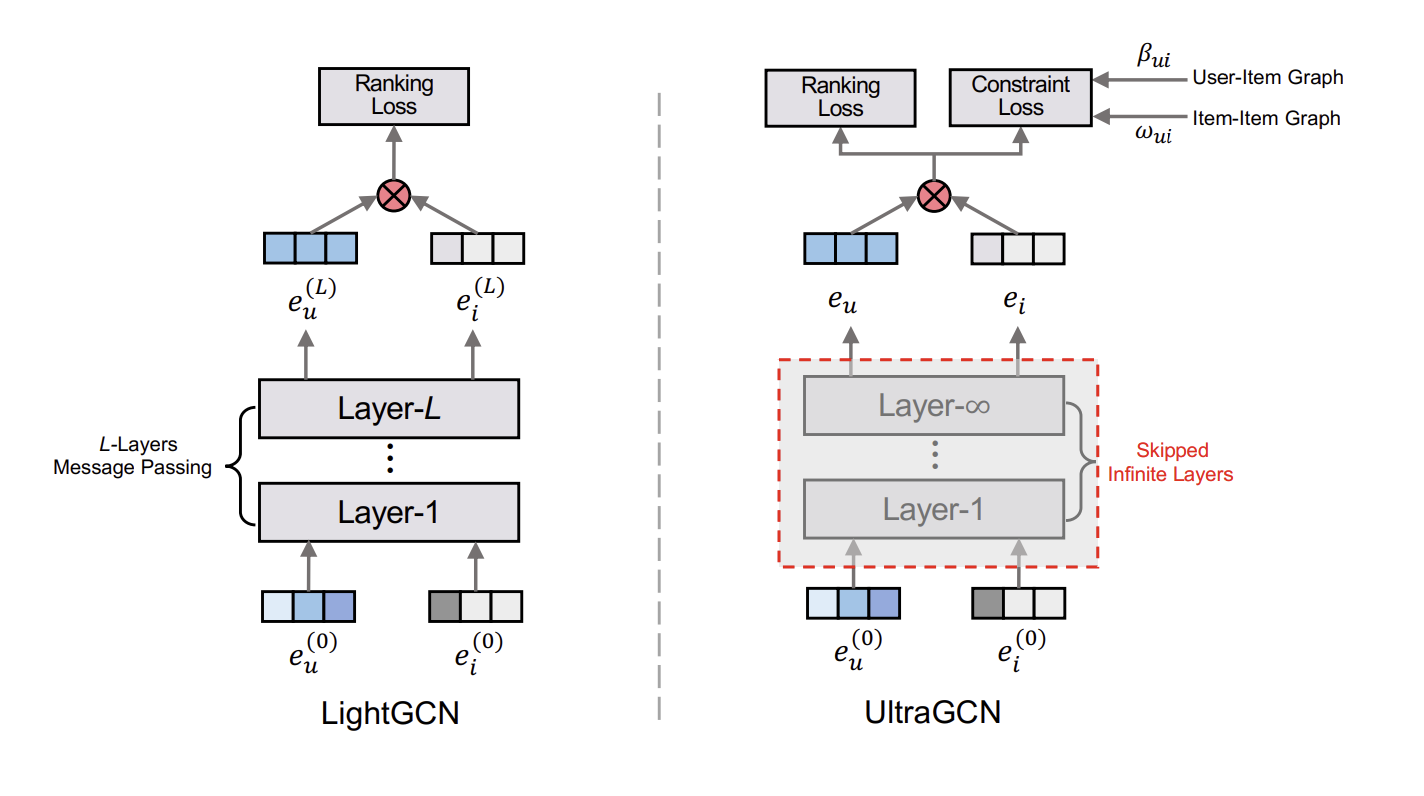
GCN의 직접적인 message passing mechanism은 학습의 수렴속도를 크게 낮춘다. 저자들이 제안한 UltraGCN은 명시적인 2~3개의 layer를 사용하는 LightGCN과 달리 무한한 layer의 근사를 사용한다. 또한 더 직관적이고 적절한 edge weight를 사용하였으며, user-item 관계, item-item 관계등 다양한 관계의 중요도를 유연히 조정할 수 있다.
Limitations of Message Passing
LightGCN에서 $l+1$번째 layer를 거친 임베딩의 내적은 아래와 같이 표현된다.
여기서 $\alpha_{ui}, \alpha_{ik}, \alpha_{uv}, \alpha_{kv}$는 아래와 같다.
여기서 GCN 기반의 모델들이 왜 효과적인지 알 수 있다. user-user 관계, item-item 관계 그리고 user-item 관계까지 서로다른 다양한 관계를 임베딩에 내포할 수 있기 때문이다.
하지만 저자들은 여기에서 3가지 한계점들을 발견한다.
weight $\alpha_{ik}$와 $\alpha_{uv}$는 합리적이지 않다.
$\alpha_{ik}$의 경우, 아이템 i와 아이템 k가 weight에 영향을 끼치는 정도가 비대칭적이다. (k의 경우 $\frac{1}{\sqrt{d_k + 1}}$이지만 i의 경우 $\frac{1}{d_i + 1}$이다.) $\alpha_{uv}$도 마찬가지의 비대칭성이 존재한다.
다양한 종류의 관계에 대한 중요도를 조절할 수 없으며, layer를 여러번 쌓으면서 불필요한 관계까지 고려하게 된다.
레이어를 많이 쌓으면 over-smoothing 문제가 발생한다.
UltraGCN - Learning on User-Item Graph
저자들은 무한한 layer를 통과한 임베딩을 직접적인 layer 적용없이 구하고자 한다. 만약 임베딩이 무한한 layer를 거쳐 수렴한 상태라면 아래와 같은 식이 성립한다.
즉, layer를 거쳐도 임베딩이 변하지 않는다는 것이다. 이는 아래와 같이 풀어쓰고 다시 정리할 수 있다.
만약 모든 임베딩에 대해 위 식이 성립하게끔 만든다면 이는 무한한 layer를 통과시킨 임베딩과 다름없다. 위 식에 근접하기 위해 좌항과 우항의 차를 직접적으로 최소화시킬 수는 있겠지만, UltraGCN에서는 normalize한 좌항과 우항의 내적을 최대화시킴으로써 이 식을 간접적으로 만족시키려 한다.
나아가 쉬운 최적화를 위해 식을 아래와 같이 변환한다.
마지막으로 over-smoothing을 방지하기 위해 negative sampling을 추가한다. (U에 대한 summation은 표기의 편의를 위해 생략하였다.) 이렇게 나온 식을 constraint loss라 하자.
Constraint loss는 단지 임베딩이 무한한 레이어를 거친 값과 동일하도록 만드는 loss이다. 임베딩의 내적이 실제 interaction에 가깝도록하는 optimization loss 또한 추가해야한다. 이는 아래와 같이 표현된다.
UltraGCN - Learning on Item-Item Graph
Contraint loss와 Optimization loss만 사용해도 충분할 수 있지만, user-item 그래프 외에도 item-item 그래프를 추가로 고려해볼 수 있다. item-item co-occurrence graph는 아래와 같이 표현된다.
즉, 두 아이템이 공유하는 유저의 수가 두 아이템 간의 edge의 weight가 된다. user-item 그래프에서도 contraint loss를 구했을 때와 마찬가지로 무한한 layer를 통과시킨 임베딩으로 만들기 위한 식을 도출할 수 있으며, 이 때의 coefficient은 아래와 같다.
이때 $G_{i,j}$는 i와 j간의 edge weight, $g_i$는 노드 i의 weighted degree를 뜻한다.
user-item 그래프 때와 달리 item-item occurence 그래프에서는 한가지 문제점이 발생하는데, 그래프가 너무 불필요하게 dense하여 부정확한 item-item 관계까지 학습한다는 것이다. 따라서 $w_{i,j}$를 기준으로 k개의 가장 유사한 item-item 관계만 고려하도록 한다. 이때 k는 hyperparameter이다.
여기서 특이한 점은 item-item 관계의 contraint를 직접적으로 학습하는 것이 아니라 item과 상호작용한 user를 거쳐서 간접적으로 학습한다는 것이다. 이는 다른 loss와의 일관성을 유지하여 학습을 더 용이하게 한다. 이의 식은 아래와 같다.
이때 집합 S(i)는 아이템 i와 유사한 k개의 아이템 집합이다.
이제 세 loss를 합친 최종적인 loss는 아래와 같이 표현된다.
이때 $\lambda$와 $\gamma$는 hyperparameter이다.